BFS是什么
核心思想:把一些问题抽象成图,从一个点开始,向四周开始扩散。
BFS 算法都是用「队列」这种数据结构,每次将一个节点周围的所有节点加入队列。
BFS和DFS的区别:BFS 找到的路径一定是最短的,但代价就是空间复杂度可能比 DFS 大很多
算法框架
BFS算法常见的场景:在一幅「图」中找到从起点 start 到终点 target 的最短路径
比如:走迷宫从起点到终点的最短路径、最少次数替换两个单词、连连看游戏…
记住框架,然后根据实际题目进行改动:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
int BFS(Node start, Node target) {
Queue<Node> q;
Set<Node> visited;
q.offer(start);
visited.add(start);
while (q not empty) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
if (cur is target)
return step;
for (Node x : cur.adj()) {
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
}
}
}
|
BFS的核心数据结构:队列 q
cur.adj() 泛指 cur 相邻的节点,比如说二维数组中,cur 上下左右四面的位置就是相邻节点;
visited 的主要作用是防止走回头路,大部分时候都是必须的,但是像一般的二叉树结构,没有子节点到父节点的指针,不会走回头路就不需要 visited。
111. 二叉树的最小深度
二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
**说明:**叶子节点是指没有子节点的节点。
示例 1:
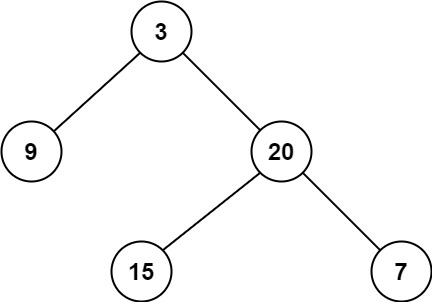
1
2
| 输入:root = [3,9,20,null,null,15,7]
输出:2
|
示例 2:
1
2
| 输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
|
提示:
- 树中节点数的范围在
[0, 105] 内
-1000 <= Node.val <= 1000
思路与算法
使用BFS框架:明确一下起点 start 和终点 target 是什么,怎么判断到达了终点?
显然起点就是 root 根节点,终点就是最靠近根节点的那个「叶子节点」,叶子节点就是两个子节点都是 null 的节点:
1
2
| if (cur.left == null && cur.right == null)
|
while 循环和 for 循环的配合,while 循环控制一层一层往下走,for 循环利用 sz 变量控制从左到右遍历每一层二叉树节点:
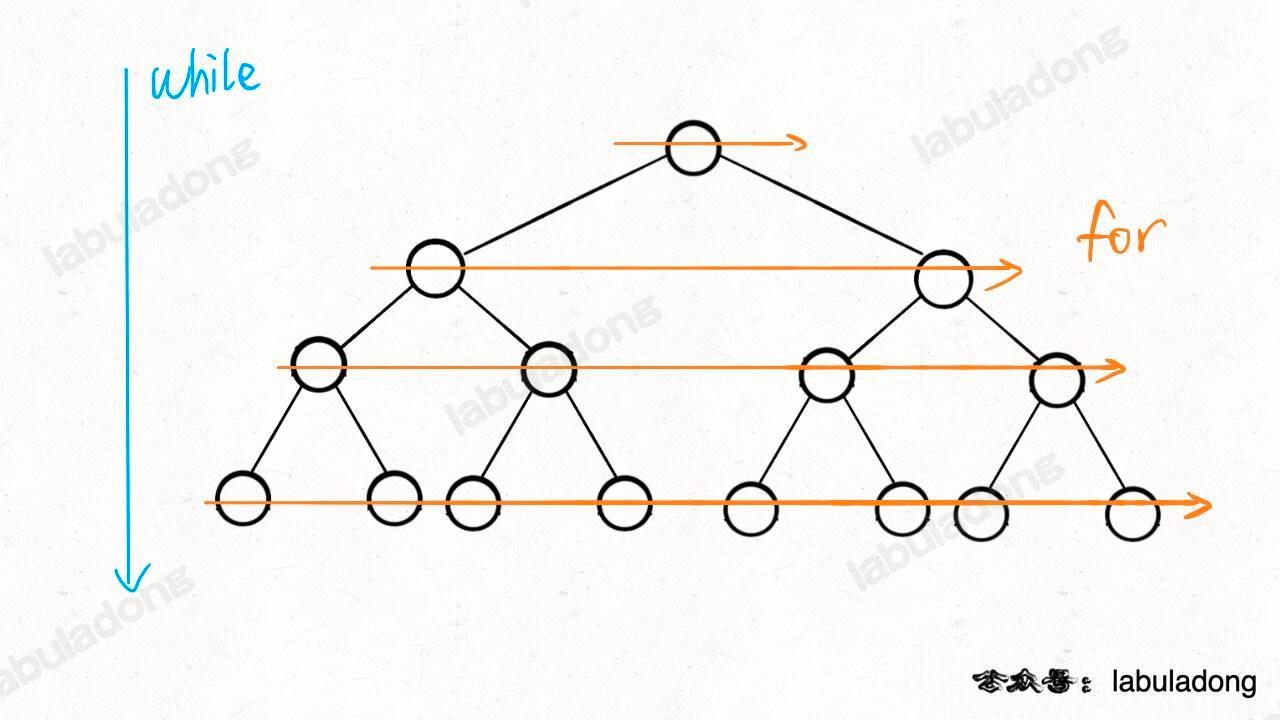
根据BFS框架解答:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public int minDepth(TreeNode root) {
if(root == null) return 0;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
int depth = 1;
while(!q.isEmpty()){
int sz = q.size();
for(int i = 0; i < sz; i++){
TreeNode cur = q.poll();
if(cur.left == null && cur.right == null) return depth;
if(cur.left != null) q.offer(cur.left);
if(cur.right != null) q.offer(cur.right);
}
depth++;
}
return depth;
}
}
|
752. 打开转盘锁
标准的BFS算法:打开转盘锁
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转:例如把 '9' 变为 '0','0' 变为 '9' 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 '0000' ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1 。
示例 1:
1
2
3
4
5
6
| 输入:deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出:6
解释:
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的,
因为当拨动到 "0102" 时这个锁就会被锁定。
|
示例 2:
1
2
3
| 输入: deadends = ["8888"], target = "0009"
输出:1
解释:把最后一位反向旋转一次即可 "0000" -> "0009"。
|
示例 3:
1
2
3
| 输入: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"
输出:-1
解释:无法旋转到目标数字且不被锁定。
|
提示:
1 <= deadends.length <= 500deadends[i].length == 4target.length == 4target 不在 deadends 之中target 和 deadends[i] 仅由若干位数字组成
思路和算法
抽象成一幅图,每个节点有 8 个相邻的节点,又让你求最短距离
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
String plusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == '9')
ch[j] = '0';
else
ch[j] += 1;
return new String(ch);
}
String minusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == '0')
ch[j] = '9';
else
ch[j] -= 1;
return new String(ch);
}
void BFS(String target) {
Queue<String> q = new LinkedList<>();
q.offer("0000");
while (!q.isEmpty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
String cur = q.poll();
System.out.println(cur);
for (int j = 0; j < 4; j++) {
String up = plusOne(cur, j);
String down = minusOne(cur, j);
q.offer(up);
q.offer(down);
}
}
}
return;
}
|
这段 BFS 代码已经能够穷举所有可能的密码组合了,但是显然不能完成题目,有如下问题需要解决:
1、会走回头路。比如说我们从 "0000" 拨到 "1000",但是等从队列拿出 "1000" 时,还会拨出一个 "0000",这样的话会产生死循环。
2、没有终止条件,按照题目要求,我们找到 target 就应该结束并返回拨动的次数。
3、没有对 deadends 的处理,按道理这些「死亡密码」是不能出现的,也就是说你遇到这些密码的时候需要跳过。
修改后:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| int openLock(String[] deadends, String target) {
Set<String> deads = new HashSet<>();
for (String s : deadends) deads.add(s);
Set<String> visited = new HashSet<>();
Queue<String> q = new LinkedList<>();
int step = 0;
q.offer("0000");
visited.add("0000");
while (!q.isEmpty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
String cur = q.poll();
if (deads.contains(cur))
continue;
if (cur.equals(target))
return step;
for (int j = 0; j < 4; j++) {
String up = plusOne(cur, j);
if (!visited.contains(up)) {
q.offer(up);
visited.add(up);
}
String down = minusOne(cur, j);
if (!visited.contains(down)) {
q.offer(down);
visited.add(down);
}
}
}
step++;
}
return -1;
}
|
 双向BFS优化
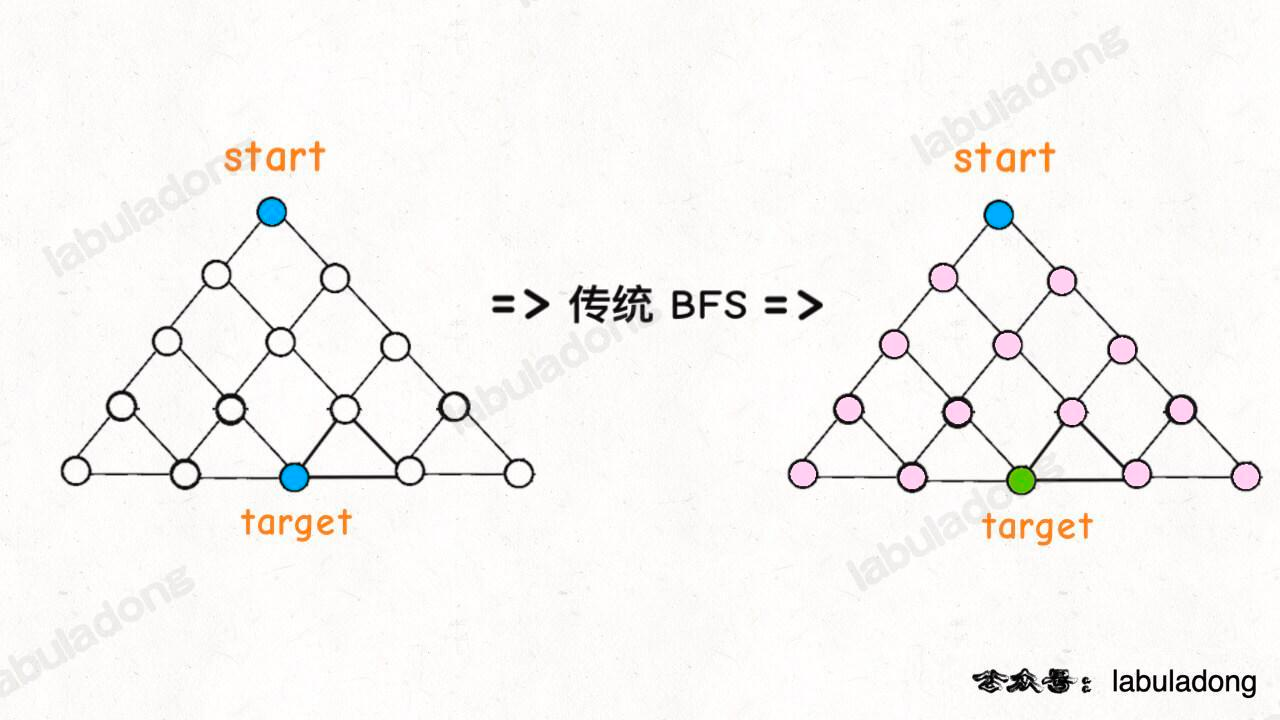
双向BFS优化
双向 BFS,可以进一步提高算法的效率
区别:传统的 BFS 框架就是从起点开始向四周扩散,遇到终点时停止;而双向 BFS 则是从起点和终点同时开始扩散,当两边有交集的时候停止。
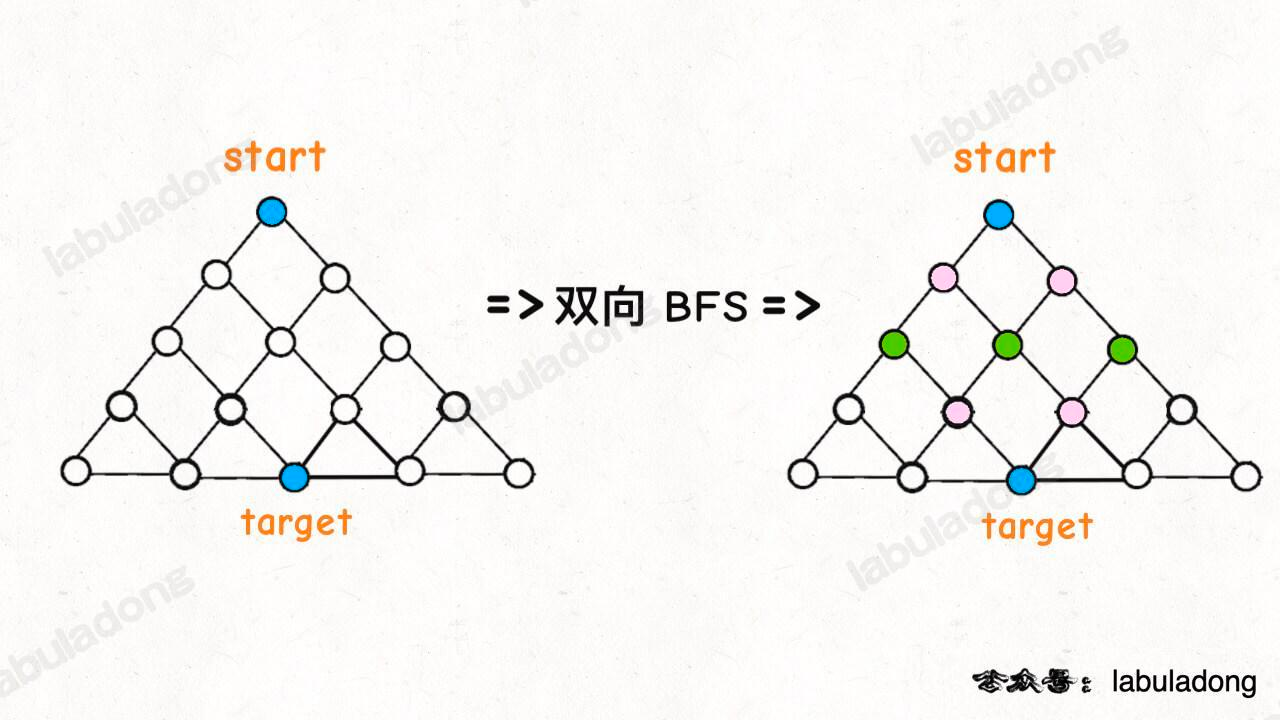
双向 BFS 也有局限,因为你必须知道终点在哪里
第二个密码锁的问题,是可以使用双向 BFS 算法来提高效率的,代码稍加修改即可:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| int openLock(String[] deadends, String target) {
Set<String> deads = new HashSet<>();
for (String s : deadends) deads.add(s);
Set<String> q1 = new HashSet<>();
Set<String> q2 = new HashSet<>();
Set<String> visited = new HashSet<>();
int step = 0;
q1.add("0000");
q2.add(target);
while (!q1.isEmpty() && !q2.isEmpty()) {
Set<String> temp = new HashSet<>();
for (String cur : q1) {
if (deads.contains(cur))
continue;
if (q2.contains(cur))
return step;
visited.add(cur);
for (int j = 0; j < 4; j++) {
String up = plusOne(cur, j);
if (!visited.contains(up))
temp.add(up);
String down = minusOne(cur, j);
if (!visited.contains(down))
temp.add(down);
}
}
step++;
q1 = q2;
q2 = temp;
}
return -1;
}
|
双向 BFS 还是遵循 BFS 算法框架的,只是不再使用队列,而是使用 HashSet 方便快速判断两个集合是否有交集。
另外的一个技巧点就是 while 循环的最后交换 q1 和 q2 的内容,所以只要默认扩散 q1 就相当于轮流扩散 q1 和 q2。
其实双向 BFS 还有一个优化,就是在 while 循环开始时做一个判断:
1
2
3
4
5
6
7
8
9
10
|
while (!q1.isEmpty() && !q2.isEmpty()) {
if (q1.size() > q2.size()) {
temp = q1;
q1 = q2;
q2 = temp;
}
|


 双向BFS优化
双向BFS优化

